Universelle Turingmaschinen

Wie im ersten Abschnitt ausgeführt wurde, läßt sich jeder Algorithmus durch eine geeignete Turingmaschinentabelle beschreiben. Die Operationstabelle läßt sich ihrerseits mechanisch interpretieren. Somit liegt der Gedanke nahe, eine Turingmaschine U zu entwickeln, welche die Operationstabelle einer beliebigen Turingmaschine T interpretieren kann und damit Tsimuliert. Eine derartige Turingmaschine U wird auch universelle Turingmaschine genannt. Eine universelle Turingmaschine entspricht in ihrer Funktionalität heutigen Universalcomputern, die beliebig neu programmiert werden können und daraufhin ihr neues Programm ausführen. Im folgenden sollen allgemeine Betrachtungen über die Möglichkeiten von Algorithmen angestellt werden. Dafür bietet die universelle Turingmaschine den besonderen Vorteil, daß man sich auf eine konkrete Operationstabelle beschränken kann und nur noch von den verschiedenen möglichen Eingaben ausgehen muß. Somit werden alle anderen Turingmaschinen durch die Möglichkeit entsprechender Eingaben für die universelle Turingmaschine mitbetrachtet.

Eine Variante des sogenannten Universal Turing Machine Theorems^4.14   ist das folgende:

Theorem Es gibt eine universelle Turingmaschine U, die die folgende zweistellige Funktion berechnet: 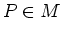$U:{\bf N}\times {\bf N}\rightarrow {\bf N}$ wobei gilt: Sei T(A) eine geeignete und berechenbare Codierung der Turingmaschinentabelle des Algorithmus A und e eine beliebige natürliche Zahl. Dann gilt U(T(A),e)=A(e). U berechnet also für seine beiden Argumente (einen Algorithmus und eine Eingabe) als Ausgabewert genau den Wert, den der Algorithmus A für die Eingabe e berechnen würde.

Soll ein bestimmter Algorithmus A auf eine gegebene Eingabezeichenkette e- zum Beispiel eine Menge von Axiomen - angewendet werden, so läßt sich dies mittels einer universellen Turingmschine U also wie folgt bewerkstelligen: Man schreibt beides, die Operationstabelle T(A) der Turingmaschinenrealisierung von A und die Eingabe e für A als Eingabe auf das Arbeitsband von U. Siehe Abbildung 3.3.

  

Abbildung 3.3: Die Eingabe zu einer universellen Turingmaschine.

Das Resultat der Anwendung des Algorithmus A auf die Eingabe e wird eine eventuell unendliche Zeichenfolge r=A(e) sein, die U in einen festgelegten Bereich ihres Arbeitsbandes schreibt. Damit kann man also eine Beziehung zwischen der Eingabe von U, nämlich T(A) verknüpft mit e und der Ausgabe r von U herstellen. Weiterhin läßt sich die Beziehung der Zahl der Eingabezeichen für U und der Länge und dem Aufbau von r herstellen. Diese Beziehung wird in der algorithmischen Informationstheorie untersucht.